The following online calculator computes
the raw outlines of two meshing non-circular gears based on the polar equation of Gear1,
the desired Gear1-to-Gear2 pitch length ratio, and desired number of teeth.
Two meshing non-circular gears can conceptually be represented by two
touching curves, called pitch or reference curves. The calculator allows the curve for Gear
1
to be specified in the form of an arbitrary mathematical function
f(u) in the polar coordinate system.
The function must define a closed, non-intersecting and smooth curve.
Below are two examples of functions which meet these requirements and are therefore suitable for non-circular gear design:
The polar equation for Gear1 is to be entered in a syntax used by all programming languages: parentheses are required with mathematical
functions, and the multiplication symbol (*) must not be omitted. Incorrect: sin 2u. Correct: sin(2*u).
The N and M parameters together specify the ratio of the lengths of Gear1's and Gear2's pitch curves.
To put it differently, when Gear1 makes N full rotations, Gear2 makes M full rotations.
The following diagram illustrates the effect of 4 different N/M combinations for this ellipse-defining function: 10 / sqrt( sin(u) * sin(u) + 5 * cos(u) * cos(u)).
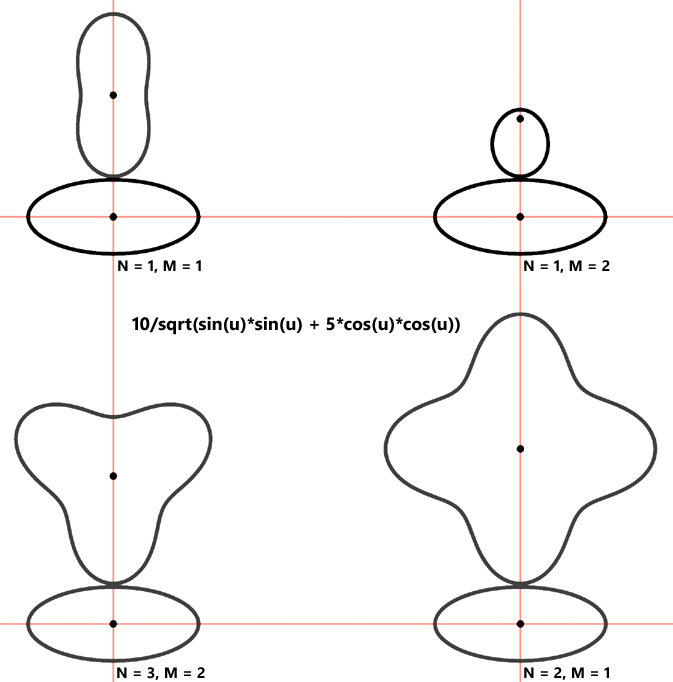
Note that the N and M values cannot be picked at random. They must reflect the periodicity of the main gear function.
The ratio N/M times the number of periods of the function must be an integer. In the example above, the periodicity of the function is 2
and therefore (N=1, M=2) and (N=3, M=2) are valid combinations. If the periodicity were, say, 1, they would not be.
The Number of Teeth (Z) must be divisible by both N and M. The actual number of teeth in Gear1 is Z / N, and in Gear2 Z / M.
The Tooth Angle (α) specifies the slanting angle of the tooth flanks. It is 20° by default.
The Tooth Height Ratio specifies the height of each tooth relative to the distance between the teeth. It is 1 by default.
Non-Circular Gear Generating Script
|